y-axis
y-coordinate
y-intercept(s)
y = mx + b
| A | B | C | D | E | F | G | H | IJK | L | M | N | O | P | Q | R | S | T | UV | WX | YZ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algebra Connections Glossary | ||||||||||||||||||||
y-axis |
|
|---|---|
| See “axes.” | |
y-coordinate |
|
| See “coordinate.” | |
y-intercept(s) |
|
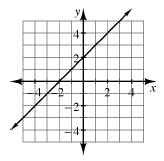
| The point(s) where a graph intersects the y-axis. A function has at most one y-intercept; a relation may have several. The y-intercept of a graph is important because it often represents the starting value of a quantity in a real-world situation. For example, on the graph of a tile pattern the y-intercept represents the number of tiles in Figure 0. We sometimes report the y-intercept of a graph with a coordinate pair, but since the x-coordinate is always zero, we often just give the y-coordinate of the y-intercept. For example, we might say that the y-intercept of the graph at right is (0, 2), or we might just say that the y-intercept is 2. When a linear equation is written in y = mx + b form, b tells us the y-intercept of the graph. For example, the equation of the graph below is y = x + 2 and its y-intercept is 2.
|
|
y = mx + b |
|
When two quantities x and y have a linear relationship, that relationship can be represented with an equation in y = mx + b form. The constant m is the slope, and b is the y-intercept of the graph. For example, the graph below shows the line represented by the equation y = 2x + 3, which has a slope of 2 and a y-intercept of 3. This form of a linear equation is also called the slope-intercept form.
|
|
zero |
|
| A number often used to represent “having none of a quantity.” Zero is neither negative nor positive. Zero is the identity element for addition. | |
Zero Product Property |
|
| The Zero Product Property states that when the product of two or more factors is zero, one of these factors must equal zero. That is, if a · b = 0, then either a = 0 or b = 0 (or both). For example, if (x + 4)(2x − 3) = 0, then either x + 4 = 0 or 2x − 3 = 0 (or both). The Zero Product Property can be used to solve factorable quadratic equations. |
|