| |
When working with an equation mat or expression comparison mat, there are certain “legal” moves you can make with the algebra tiles that keep the relationship between the two sides of the mat intact. For example, removing an x tile from the positive region of each side of an equation mat is a legal move; it keeps the expressions on each side of the mat equal. The legal moves are those justified by the properties of the real numbers. |
less than |
| |
(1) One expression is less than another if its value is not as large. We indicate this relationship with the less than symbol “<”. For example, 1 + 1 is less than 4 + 5. We write 1 + 1 < 4 + 5. (p. 377) (2) We sometimes say that one amount is a certain quantity less than another amount. For example, a student movie ticket might cost two dollars less than an adult ticket. |
“let” statement |
| |
A “let” statement is written at the beginning of our work to identify the variable that will represent a certain quantity. For example, in solving a problem about grilled cheese sandwiches, we might begin by writing “Let s = the number of sandwiches eaten.” It is particularly important to use “let” statements when writing mathematical sentences, so that your readers will know what the variables in the sentences represent. |
like terms |
| |
Two or more terms that contain the same variable(s), with corresponding variables raised to the same power. For example, 5x and 2x are like terms. (Also see “combiningliketerms.”) |
line of symmetry |
| |
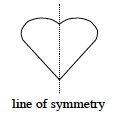
A line that divides a shape into two pieces that are mirror images of each other. If you fold a shape over its line of symmetry, the shapes on both sides of the line will match perfectly. A shape with a line of symmetry is shown below.
 |
linear equation |
| |
An equation in two variables whose graph is a line. For example, y = 2.1x − 8 is a linear equation. The standard form for a linear equation is ax + by = c, where a, b, and c are constants and a and b are not both zero. Most linear equations can be written in
y = mx + b form, which is more useful for determining the line’s slope and y-intercept. |
looking inside |
| |
“Looking inside” is a method of solving one-variable equations containing parentheses or an absolute value symbol. To use “looking inside,” we first determine what the value of the entire expression inside the parentheses (or absolute value symbol) must be. We then use that fact to solve for the value of the variable. For example, to use “looking inside” to solve the equation 4(x + 2) = 36, we first determine that x + 2 must equal 9. We then solve the equation
x + 2 = 9 to find that x = 7. |

