AC Glossary

A	B	C	D	E	F	G	H	IJK	L	M	N	O	P	Q	R	S	T	UV	WX	YZ
Algebra Connections Glossary

scale on axes
	The scale on an axis tells you what number each successive mark on the axis represents. A complete graph has the scale marked with numbers on each axis. Each axis should be scaled so that each interval represents the same amount.
scientific notation
	A number is expressed in scientific notation when it is in the form , where 1 < a < 10 and n is an integer. For example, the number 31,000 can be expressed in scientific notation as .
similar figures
	Similar figures have the same shape but are not necessarily the same size. For example the two triangles below are similar. In similar figures, the measures of corresponding angles are equal and the lengths of corresponding sides are proportional.
simple radical form

simplify
	A number is in simple radical form if no square of an integer divides s and s is not a fraction; that is, there are no perfect square factors (square numbers such as 4, 9, 16, etc.) under the radical sign and no radicals in the denominator. For example, is not in simple radical form since 4 (the square of 2) divides 12. But is in simple radical form and is equivalent to .
	To simplify an expression is to write a less complicated expression with the same value. A simplified expression has no parentheses and no like terms. For example, the expression 3 − (2x + 7) − 4x can be simplified to −4 − 6x. When working with algebra tiles, a simplified expression uses the fewestpossible tiles to represent the original expression.
slope
	so that describes how steep (or flat) a line is. Slope can be positive, negative, or even zero, but a straight line has only one slope. Slope is the ratio or , sometimes written . When the equation of a line is written in y = mx + b form, m is the slope of the line. Some texts refer to slope as the ratio of the “rise over the run.” A line has positive slope if it slopes upward from left to right on a graph, negative slope if it slopes downward from left to right, zero slope if it is horizontal, and undefined slope if it is vertical.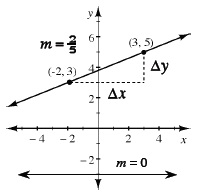
slope-intercept form

slope triangle
	See “y = mx + b.”
	A slope triangle is a right triangle drawn on a graph of a line so that the hypotenuse of the triangle is part of the line. The vertical leg length is the change in the y-value (Δy); the horizontal leg length is the change in the x-value (Δx). We use the lengths of the legs in the triangle to calculate the slope ratio . For example, the diagram below shows a slope triangle with Δy = 2, Δx = 4. The slope of the line in the example is , or . (Also see “slope.”)
solution
	The number or numbers that when substituted into an equation or inequality make the equation or inequality true. For example, x = 4 is a solution to the equation 3x − 2 = 10 because 3x − 2 equals 10 when x = 4. A solution to a two-variable equation is sometimes written as an ordered pair (x, y). For example, x = 3 and y = −2 is a solution to the equation y = x − 5; this solution can be written as (3, −2).
solve
	(1) To find all the solutions to an equation or an inequality (or a system of equations or inequalities). For example, solving the equation x² = 9 gives the solutions x = 3 and x = −3. (pp. 68, 119, 170) (2) Solving an equation for a variable gives an equivalent equation that expresses that variable in terms of other variables and constants. For example, solving 2y − 8x = 16 for y gives y = 4x + 8. The equation y = 4x + 8 has the same solutions as 2y − 8x = 16, but y = 4x + 8 expresses y in terms of x and some constants.
square numbers
	The numbers in the pattern 1, 4, 9, 16, 25, … . That is, the squares of the counting numbers 1, 2, 3, 4, 5, ... are known as square numbers.
square root
	A number a is a square root of b if a² = b. For example, the number 9 has two square roots, 3 and −3. A negative number has no real square roots; a positive number has two; and zero has just one square root, namely, itself. Other roots, such as cube root, will be studied in other courses. (Also see “radical.”)

standard form for a number
	See “standard notation.”
standard form for quadratics
	A quadratic expression in the form ax² + bx + c is said to be in standard form. For example, the following are all expressions in standard form: 3m² + m − 1, x² − 9, and 3x² + 5x.
standard form of a linear equation
	The standard form for a linear equation is ax + by = c, where a, b, and c are real numbers and a and b are not both zero. For example, the equation 2.5x − 3y = 12 is in standard form. When you are given the equation of a line in standard form, it is often useful to write an equivalent equation in y = mx + b form to find the line’s slope and y-intercept.
standard notation

starting value
	A number written out completely, showing all digits and without use of exponents is written in standard notation. For example, 31,000 is the standard notation for the number expressed by . Standard notation is also sometimes called “standard form.”
	In certain situations, the dependent variable has a starting value where the situation described in a problem begins. For example, if we are measuring the population of a town over time, that population will have some starting value when we begin our measurements.
substitution
	Replacing one symbol with a number, a variable, or another algebraic expression of the same value. Substitution does not change the value of the overall expression. For example, suppose we are trying to evaluate the expression 13x − 6 when x = 4. Since x has the value 4, we can substitute 4 into the expression wherever x appears, giving us the equivalent expression 13(4) − 6.
Substitution Method

Substitution Property
	A method for solving a system of equations by replacing one variable with an expression involving the remaining variable(s). For example, in the system of equations at right the first equation tells you that y is equal to −3x + 5. We can substitute −3x + 5 in for y in the second equation to get 2(−3x + 5) + 10x = 18, then solve this equation to find x. Once we have x, we substitute that value back into either of the original equations to find the value of y.
	The Substitution Property states that if a = b, a can be replaced by b in any expression without changing the value of the expression. For example, if x = 4, 13x − 6 has the same value as 13(4) − 6.
sum
	The result of adding two or more numbers. For example, the sum of 4 and 5 is 9.
Symmetric Property of Equality
	The Symmetric Property states that if two expressions are equal, it does not matter which is stated first. That is, if a = b then b = a. For example, 56 ÷ 8 = 7, and 7 = 56 ÷ 8.

symmetry
	See “line of symmetry.”
system of equations
	A system of equations is a set of equations with the same variables. Solving a system of equations means finding one or more solutions that make each of the equations in the system true. A solution to a system of equations gives a point of intersection of the graphs of the equations in the system. There may be zero, one, or several solutions to a system of equations. For example, (1.5, −3) is a solution to the system of equations below; setting x = 1.5, y = −3 makes both of the equations true. Also, (1.5, −3) is a point of intersection of the graphs of these two equations.
system of inequalities
	A system of inequalities is a set of inequalities with the same variables. Solving a system of inequalities means finding one or more regions on the coordinate plane whose points represent solutions to each of the inequalities in the system. There may be zero, one, or several such regions for a system of inequalities. For example, the shaded region at right is a graph of the system of inequalities that appears below it.