A B C D E F G H IJK L M N O P Q R S T UV WX YZ
Algebra Connections Glossary
closure properties of rational numbers 
  The closure properties of rational numbers state that the product or sum of two rational numbers is a rational number.  For example, pic and pic are both rational numbers; pic is pic; and pic is a rational number.  Also, 2.2 and 0.75 are both rational numbers; 2.2 · 0.75 is 1.65; and 1.65 is a rational number.
coefficient (numerical)   
  A number multiplying a variable or product of variables.  For example, −7 is the coefficient of −7xy².
coincide   
  Two graphs coincide if they have all their points in common.  For example, the graphs of y = 2x + 4 and 3y = 6x + 12 coincide; both graphs are lines with a slope of 2 and a y-intercept of 4.  When the graphs of two equations coincide, those equations share all the same solutions and have an infinite number of intersection points.
combining like terms   
  Combining two or more like terms simplifies an expression by summing constants and summing those variable terms in which the same variables are raised to the same power.  For example, combining like terms in the expression 3x + 7 + 5x − 3 + 2x² + 3y² gives 8x + 4 + 2x² + 3y².  When working with algebra tiles, combining like terms involves putting together tiles with the same dimensions.
common denominator   
  A common denominator of a group of fractions is an expression that has the denominators of each of the fractions as a factor.  For example, if we are simplifying the sum pic, we might use 14(x + 3) as a common denominator for all three terms.
common factor   
  A common factor is a factor that is the same for two or more terms.  For example, x² is a common factor of 3x² and −5x²y.
Commutative Property of Addition   
  The Commutative Property of Addition states that if two terms are added, the order can be reversed with no effect on the total.  That is, a + b = b + a.  For example, 7 + 12 = 12 + 7.
Commutative Property of Multiplication   
  The Commutative Property of Multiplication states that if two expressions are multiplied, the order can be reversed with no effect on the result.  That is, ab = ba.  For example, 5 · 8 = 8 · 5.
complete graph   
  A complete graph includes all the necessary information about a line or a curve.  To be complete, a graph must have the following components:  (1) the x-axis and y-axis labeled, clearly showing the scale;  (2) the equation of the graph written near the line or curve;  (3) the line or curve extended as far as possible on the graph with arrows if the line or curve continues beyond the axes;  (4) the coordinates of all special points, such as x- and y-intercepts, shown in (x, y) form.

pic

 

 

completing the square   
  In this course, we use completing the square to convert a quadratic equation in standard form into perfect square form.  To complete the square, we add (or subtract) a constant to (or from) both sides of the equation so that the quadratic expression can be factored into a perfect square.  For example, when given the quadratic equation x² − 6x + 4 = 0, we can complete the square by adding 5 to both sides.  The resulting equation, x² − 6x + 9 = 5, has a left-hand side we can factor, resulting in the perfect square form quadratic equation (x − 3)² = 5.
conclusion   
  In an “If...then...” statement, the “then” portion is called the conclusion.  For example, in the statement “If x = 3, then x² = 9,” the conclusion is
“x² = 9.” (Also see “hypothesis.”)
consecutive numbers   
  Integers that are in order without skipping any of them.  For example, 8, 9, and 10 are consecutive numbers.
congruent  
  Two shapes are congruent if they have exactly the same size and shape.  For example, the two triangles below are congruent.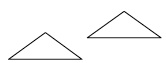pic
constant   
  A symbol representing a value that does not change.  For example, in the equation y = 2x + 5, the number 5 is a constant.
continuous graph   
 

A graph whose points are connected with an unbroken line or curve is called a continuous graph.  A continuous graph can be traced with a pencil without ever lifting the pencil to move from one point on the graph to another point.  For example, the graphs shown below are both continuous.  (Also see “discrete.”)

pic
coordinate(s)   
  The number corresponding to a point on the number line or an ordered pair (x, y) that corresponds to a point in a two-dimensional coordinate system.  In an ordered pair, the x-coordinate appears first and the y-coordinate appears second.  For example, the point (3, 5) has an x-coordinate of 3.
coordinate plane   
  A flat surface defined by two number lines meeting at  right angles at their zero points.  A coordinate plane is also sometimes called a “Cartesian Plane.”
coordinate system   
  A system of graphing ordered pairs of numbers on a coordinate plane.  An ordered pair represents a point, with the first number giving the horizontal position relative to the x-axis and the second number giving the vertical position relative to the y-axis.  For example, the diagram below shows the point (3, 5) graphed on a coordinate plane.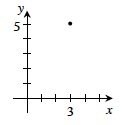piocpic
counterexample   
  An example showing that a statement has at least one exception; that is, a situation in which the statement is false.  For example, the number 4 is a counterexample to the hypothesis that all even numbers are greater than 7.