AC Glossary

A	B	C	D	E	F	G	H	IJK	L	M	N	O	P	Q	R	S	T	UV	WX	YZ
Algebra Connections Glossary

radical
	An expression in the form , where is the positive square root of a. For example, . (Also see “square root.”)
radicand
	The expression under a radical sign. For example, in the expression , the radicand is x − 7.
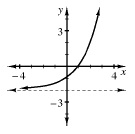
range
	The set of all output values for a function or relation. For example, the range of the function graphed below is y > −2. (Also see “domain.”)
ratio

rational expression
	A ratio compares two quantities by division. A ratio can be written using a colon, but is more often written as a fraction. For example, we might be interested in the ratio of female students in a particular school to the total number of students in the school. This ratio could be written as 1521:2906 or as the fraction shown at below.
	An expression in the form of a fraction in which the numerator and/or denominator contain polynomials. For example, is a rational expression.
rational numbers
	Numbers that can be expressed in the form , where a and b are integers and b ≠ 0. For example, 0.75 is a rational number because it can be expressed in the form .
real numbers

reciprocal
	Irrational numbers together with rational numbers form the set of the real numbers. For example, the following are all real numbers: . All real numbers are represented on the number line.
	The reciprocal of a nonzero number is its multiplicative inverse; that is, the reciprocal of x is . For a number in the form , where a and b are non-zero, the reciprocal is . The product of a number and its reciprocal is 1. For example, the reciprocal of 12 is , and . (Also see “Multiplicative Inverse Property.”)
Reflexive Property
	The Reflexive Property states that any expression is always equal to itself. That is, a = a. For example, 1627x² − 2 = 1627x² − 2.
relation
	An equation that relates inputs to outputs. For example, and x² + y² = 18 are both relations. The set of input values to a relation is the domain, and the set of output values is the range. A relation can also be thought of as a set of ordered pairs.
representation
	A representation expresses a relationship between quantities in a particular way. In this course, we emphasize four different ways of representing a numerical relationship: with a graph, table, situation (pattern), or rule (equation or inequality). (Also see “representations web.”)
representations web
	The representations web, or just “the web,” is an organizational tool we use to keep track of connections between the four representations of numerical relationships emphasized in this course. As we learn how to move from one representation of a particular type of pattern to another, we record this by drawing an arrow on the web. For example, an arrow from “rule” to “graph” in the web might record our ability to draw the graph for a given equation. (Also see “representation.”)

rewriting
	To rewrite an equation or expression is to write an equivalent equation or expression. In this course, “rewriting” also refers to a method of solving one-variable equations. In “rewriting,” we use algebraic techniques to write an equation equivalent to the original. This will often involve using the Distributive Property to eliminate parentheses. We then solve the equation using various solution methods, including perhaps rewriting again. For example, to solve the equation 4(x + 2) = 36 by “rewriting,” we use the Distributive Property to rewrite the equation as 4x + 8 = 36. We then solve this equation to find that x = 7.
root
	A root of an equation is a solution of the equation. For example, the roots of (x − 4)(2x + 3) = 0 are x = 4 and . When working with a function f(x), the x-intercepts of the function’s graph are the roots of the equation f(x) = 0.
rule
	A rule is an equation or inequality that represents the relationship between two numerical quantities. We often use a rule to represent the relationship between quantities in a table, a pattern, a real-world situation, or a graph. For example, the rule y = 0.4x + 25 might tell us how to find the total cost y in cents of talking on a pay phone for x minutes.