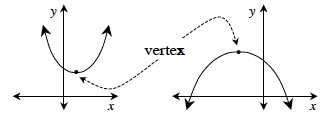
parabola
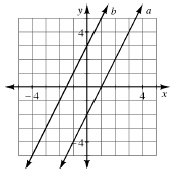
parallel
= 2x + 3 and y = 2x − 2 are parallel (see diagram at right). When two equations have parallel graphs, the equations have no solutions in common.
pattern
percent
| A | B | C | D | E | F | G | H | IJK | L | M | N | O | P | Q | R | S | T | UV | WX | YZ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algebra Connections Glossary | ||||||||||||||||||||
parabola |
|
|---|---|
| A parabola is a particular kind of mathematical curve. In this course, a parabola is always the graph of a quadratic function y = ax² + bx + c where a does not equal 0. The diagram below shows some examples of parabolas. The highest or lowest point on the graph is called thevertex.
|
|
parallel |
|
| Two or more straight lines on a flat surface that do not intersect (no matter how far they are extended) are parallel. If two lines have the same slope and do not coincide, they are parallel. For example, the graphs of y = 2x + 3 and y = 2x − 2 are parallel (see diagram at right). When two equations have parallel graphs, the equations have no solutions in common.
|
|
pattern |
|
| A pattern is a set of things in order that change in a regular way. For example, the numbers 1, 4, 7, 10, … form a pattern, because each number increases by 3. The numbers 1, 4, 9, 16, … form a pattern, because they are squares of consecutive integers. (p. 96) In this course, we often look at tile patterns, whose figure numbers and areas we represent with a table, a rule (equation), or a graph.
|
|
percent |
|
| A ratio that compares a number to 100. Percents are often written using the “%” symbol. For example, 0.75 is equal to |
|
perfect square form |
|
| A quadratic equation in the form a(x + b)² = c, where a is nonzero, is said to be in perfect square form. For example, 3(x − 12)² = 19 is a quadratic equation in perfect square form. | |
perfect square trinomials |
|
| Trinomials of the form a²x² + 2abx + b², where a and b are nonzero real numbers, are known as perfect square trinomials and factor as (ax + b)². For example, the perfect square trinomial 9x² − 24x + 16 can be factored as (3x − 4)². | |
perimeter |
|
| The distance around a figure on a flat surface. | |
perpendicular |
|
| Two lines or segments that meet (intersect) to form a 90˚ angle. For example, the lines shown on the graph below are perpendicular. If two perpendicular lines are graphed in an xy‑coordinate system, their slopes are opposite reciprocals.
|
|
point of intersection |
|
| A point of intersection is a point that the graphs of two equations have in common. For example, (3, 4) is a point of intersection of the two graphs shown below. Two graphs may have one point of intersection, several points of intersection, or no points of intersection. The ordered pair representing a point of intersection gives a solution to the equations of each of the graphs.
|
|
point-slope form |
|
| The point-slope form of the equation of a line is y − k = m(x − h), where (h, k) are the coordinates of a point on the line, and m is the slope of the line. For example, a line with slope −4 passing through the point (5, 8) has the equation y − 8 = −4(x − 5). To find the equation of the line in y = mx + b form, we solve the point-slope form equation for y. | |
polygon |
|
A two-dimensional closed figure of straight line segments (“edges” or “sides”) connected end to end. Each side (or edge) intersects only the endpoints of its two adjacent sides (or edges). For example, the shape below is a polygon. 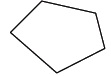 |
|
polynomial |
|
| An expression that is the sum or difference of two or more monomials (terms). For example, |
|
power |
|
|---|---|
| A number or variable raised to an exponent in the form |
|
prediction |
|
| A rule (equation), table, or graph can be used to make a prediction about the value(s) a quantity will take that we have not yet seen. For example, we might analyze data about the height of a tree in each of its first three years of growth to predict how tall it will be at the end of year 4. | |
prime number |
|
| A positive integer with exactly two factors. The only factors of a prime number are 1 and itself. For example, the numbers 2, 3, 17, and 31 are all prime. 31 has no factors other than 1 and 31. | |
problem-solving strategies |
|
| This course incorporates several problem-solving strategies, specifically, making a guess and checking it, using manipulatives (such as algebra tiles), making systematic lists, collecting data, graphing, drawing a diagram, breaking a large problem into smaller subproblems, working backward, and writing and solving equations. For example, a student given the details of a cell-phone pricing plan and asked how many minutes would cost $29.95 might approach the problem by writing an equation and solving it, making a table of times and prices, graphing the relationship, or guessing and checking various numbers of minutes. | |
product |
|
| The result of multiplying. For example, the product of 4 and 5 is 20; the product of 3a and 8b² is 24ab². | |
proportion |
|
| An equation stating that two ratios (fractions) are equal. For example, the equation below is a proportion. A proportion is a useful type of equation to set up when solving problems involving proportional relationships.
|
|