A B C D E F G H IJK L M N O P Q R S T UV WX YZ
Algebra Connections Glossary
deductive reasoning 
 

See “justify.”
degree   
  (1) The degree of a monomial is the sum of the exponents of its variables.  For example, pic has degree 7, because the sum of the exponents (5 + 2) is 7.   (2) The degree of a polynomial in one variable is the degree of the term with the highest exponent.  For example, pichas degree 5, because the highest exponent to which x is raised is 5.   (3) The degree of a polynomial in more than one variable is the highest sum of the exponents among the terms.  For example, pic has degree 9, because the sum of the exponents in the second term is 9 and no term has a higher exponent sum.
dependent variable   
  When one quantity depends for its value on one or more others, it is called the dependent variable.  For example, we might relate the speed of a car to the amount of force you apply to the gas pedal.  Here, the speed of the car is the dependent variable; it depends on how hard you push the pedal.  The dependent variable appears as the output value in an x ® y table, and is usually placed relative to the vertical axis of a graph.  We often use the letter y for the dependent variable.  When working with functions or relations, the dependent variable represents the output value. (Also see “independent variable.”)
difference of squares   
  A polynomial that can be factored as the product of the sum and difference of two terms. The general pattern is x² −y² = (x +y)(x − y).  Most of the differences of squares found in this course are of the form a²x² − b² = (ax + b)(ax − b), where a and b are nonzero real numbers.  For example, the difference of squares 4x² − 9 can be factored as (2x + 3)(2x − 3).
dimensions   
 

The dimensions of a flat region or space tell how far it extends in each direction.  For example, the dimensions of a rectangle might be 16 cm wide by 7 cm high.

discrete graph   
  A graph that consists entirely of separated points is called a discrete graph.  For example, the graph shown at right is discrete.  (Also see “continuous.”) 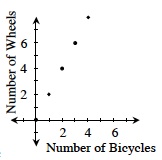pic
discriminant   
  For quadratic equations in standard form ax² + bx + c = 0, the discriminant is b − 4ac.  If the discriminant is positive, the equation has two roots; if the discriminant is zero, the equation has one root; if the discriminant is negative, the equation has no real-number roots.  For example, the discriminant of the quadratic equation 2x² − 4x − 5 is (−4)² − 4(2)(−5) = 56, which indicates that that equation has two roots (solutions).
Distributive Property   
  We use the Distributive Property to write a product of expressions as a sum of terms.  The Distributive Property states that for any numbers or expressions a, b, and c, a(b + c) = ab + ac.  For example,
2(x + 4) = 2 · x + 2 · 4 = 2x + 8.  We can demonstrate this with algebra tiles or in a generic rectangle. 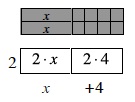pic
dividing line   
  See “boundary line.”  
dividing point   
  See “boundary point.”
domain   
  The set of all input values for a relation or function.  For example, the domain of the function graphed at right is x > −3.   For variables, the domain is the set of numbers the variable may represent.  (Also see “range.”)

pic