edge
endpoint
enlargement ratio
equal (=)
| A | B | C | D | E | F | G | H | IJK | L | M | N | O | P | Q | R | S | T | U | V | WXYZ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Making Connections Glossary | |||||||||||||||||||||
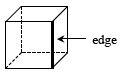
edge |
|
|---|---|
In three dimensions, a line segment formed by the intersection of two faces of a polyhedron. |
|
endpoint |
|
| Either of the two points that mark the ends of a line segment. (Also see line segment.) | |
enlargement ratio |
|
| The ratio of similarity comparing a figure to a similar larger figure is often called the enlargement ratio. This ratio shows by what factor the first figure is enlarged to get the second figure. | |
equal (=) |
|
| Two quantities are equal when they have the same value. For example, when x = 4, the expression x + 8 is equal to the expression 3x because the values of the expressions are the same. | |
equal ratios |
|
| Two equivalent fractions, also called a proportion. For example, |
|
equation |
|
| A mathematical sentence in which two expressions appear on either side of an “equals” sign (=), stating that the two expressions are equivalent. For example, the equation 7x + 4.2 = − 8 states that the expression 7x + 4.2 has the value –8. In this course, an equation is often used to represent a rule relating two quantities. For example, a rule for finding the area y of a tile pattern with figure number x might be written y = 4x − 3. | |
equilateral |
|
A polygon is equilateral if all of its sides have equal length. The word “equilateral” comes from “equi” (meaning “equal”) and “lateral” (meaning “side”). Equilateral triangles not only have sides of equal length, but also angles of equal measure. However, a polygon with more than three sides may be
equilateral without having congruent angles. For example, see the rhombus below. 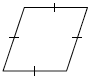 |
|
equivalent |
|
| Two expressions are equivalent if they have the same value. For example, 2 + 3 is equivalent to 1 + 4. Two equations are equivalent if they have all the same solutions. For example, y = 3x is equivalent to 2y = 6x. Equivalent equations also have the same graph. | |
equivalent fractions |
|
| Two fractions are equivalent if they have the same numerical value. For example, 3/6 and 5/10 are equivalent fractions. | |
evaluate (an expression) |
|
| To find the numerical value of. To evaluate an expression, substitute the value(s) given for the variable(s) and perform the operations according to the order of operations. For example, evaluating 2x + y − 10 when x = 4 and y = 3 gives the value 1. (Also see expression.) | |
even number |
|
| A whole number that is divisible by two with no remainder. | |
event |
|
| One or more results of an experiment. | |
experimental probability |
|
| The probability based on data collected in experiments. The experimental probability of an event is defined to be |
|
exponent |
|
| In an expression of the form ab, b is called the exponent. For example, in the expression 25, 5 is called the exponent (2 is the base, and 32 is the value). The exponent indicates how many times to use the base as a multiplier. For example, in 25, 2 is used 5 times: 25 = 2 · 2 · 2 · 2 · 2 = 32. For exponents of zero, the rule is: for any number x ≠ 0, x0 = 1. | |
expression |
|
| An expression is a combination of individual terms separated by plus or minus signs. For example, if each of the following terms, 6xy², 24, and |
|
expression mat |
|
An organizing tool used to visually represent an expression with algebra tiles. An expression mat has two regions, a positive region at the top and a negative region at the bottom. The tiles on the expression mat at right represent a value of –3.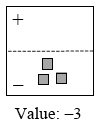 |
|