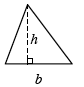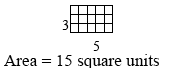5-D process |
| |
An organized method to solve problems. The 5 D’s stand for Describe/Draw, Define, Do, Decide, and Declare. This is a problem-solving strategy for which solving begins by making a prediction, and then confirming whether or not the result is correct. If not, information is gained about how close the trial is to the correct value, so that adjustments may be made. Being organized is extremely important to the success of this method, as well as writing a usable table. The 5-D process leads to writing equations to represent word problems. |
absolute value |
| |
The absolute value of a number is the distance of the number from zero. Since the absolute value represents a distance, without regard to direction, absolute value is always non-negative. Thus, the absolute value of a negative number is its opposite, while the absolute value of a non-negative number is just the number itself. The absolute value of x is usually written “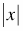 .” For example, | .” For example, |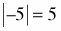 and and  . . |
acute angle |
| |
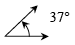
An angle with a measure greater than 0º and less than 90º. An example is shown below.
 |
acute triangle |
| |
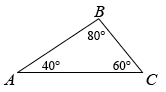
A triangle with all three angle measures less than 90º.
 |
addition ( ) ) |
| |
An operation that tells how many objects there are when two sets are combined. The result is the number of objects in the two sets together which is called a sum. In arithmetic, the word “object” usually means “number.” |
Additive Inverse Property |
| |
The additive inverse property states that for every number a there is a number –a such that a + (−a) = 0. For example, the number 5 has an additive inverse of –5; 5 + (−5) = 0. The additive inverse of a number is often called its opposite. For example, 5 and
–5 are opposites. |
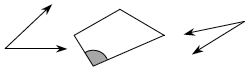
adjacent angles |
| |
For two angles to be adjacent, the angles must satisfy these three conditions: (1) the two angles must have a common side; (2) the two angles must have a common vertex; and (3) the two angles may have no interior points in common. Meeting these three conditions means that the common side must be between the two angles. No overlap between the angles is permitted. In the example at right, ∡ABC and ∡CBD are adjacent angles.
 |
algebra |
| |
A branch of mathematics that uses variables to generalize the rules of numbers and numerical operations. |
algebra tiles |
| |
An algebra tile is a manipulative whose area represents a constant or variable quantity. The algebra tiles used in this course consist of large squares with dimensions x-by- x and y-by- y; rectangles with dimensions x-by-1, y-by-1, and x-by- y; and small squares with dimensions 1-by-1. These tiles are named by their areas: x², y², x, y, xy, and 1, respectively. The smallest squares are called “unit tiles.” In this text, shaded tiles will represent positive quantities while unshaded tiles will represent negative quantities. 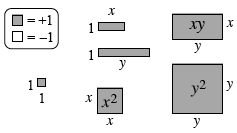 |
algebraic expression |
| |
See expression. |
algorithm |
| |
A fixed rule for carrying out a mathematical procedure. For example, to find the average of a set of values, find the sum of the values and divide by the number of values.
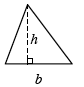
|
altitude of a triangle |
| |
The length of a segment that connects a vertex of the triangle to a line containing the opposite base (side) and is perpendicular to that line. (See height.) |
angle |
| |
Generally, an angle is formed by two rays that are joined at a common endpoint. Angles in geometric figures are usually formed by two segments that have a common endpoint (such as the angle shaded in the figure at right). (Also see acute angle, obtuse angle, and right angle.)
|
angle bisector |
| |
A ray that divides an angle into two congruent parts. |
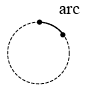
arc |
| |
A part of a circle or curve between two points on the circle.
 |
area |
| |
For this course, area is the number of square units needed to fill up a region on a flat surface. In later courses, the idea will be extended to cones, spheres, and more complex surfaces.
(Also see surface area.)
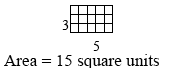 |
area of a circle |
| |
A = πr², where r is the length of the radius of the circle. (See “circle.”) |
area of a triangle |
| |
To find the area of a triangle, multiply the length of the base b by the height h and divide by two: A=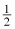 bh . (Also see altitude of a triangle.) bh . (Also see altitude of a triangle.) |
Associative Property for Addition |
| |
The associative property of addition states that if a sum contains terms that are grouped, then the sum may be grouped differently with no effect on the total, that is, a + (b + c) = (a + b) + c. For example, 3 + (4 + 5) = (3 + 4) + 5. |
Associative Property for Multiplication |
| |
The associative property of multiplication states that if a product contains terms that are grouped, then the product may be grouped differently with no effect on the result, that is, a(bc) = (ab)c. For example, 2·(3·4) = (2·3)·4. |
average |
| |
The sum of given values divided by the number of values used in computing the sum.
For example, the average of 1, 4, and 10 is (1+4+10) / 3. (See mean.)
|
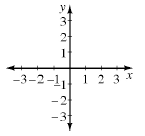
axis (plural: axes) |
| |
In a coordinate plane, two number lines that meet at right angles at the origin (0, 0).
The x-axis runs horizontally and the y-axis runs vertically.
 |
|

 )
)